วิธีคูณทศนิยม. เศษส่วน การคูณทศนิยม ตำแหน่งเป็นทศนิยม

เพื่อให้เข้าใจวิธีการคูณทศนิยม มาดูตัวอย่างกัน

กฎการคูณ เศษส่วนทศนิยม

1) เราคูณโดยไม่สนใจลูกน้ำ

2) ด้วยเหตุนี้ เราจึงแยกตัวเลขหลังเครื่องหมายจุลภาคให้มากที่สุดเท่าที่มีหลังเครื่องหมายจุลภาคในทั้งสองปัจจัยรวมกัน

ตัวอย่าง.

ค้นหาผลคูณของทศนิยม:

ในการคูณทศนิยม เราจะคูณโดยไม่ต้องสนใจเครื่องหมายลูกน้ำ นั่นคือเราไม่ได้คูณ 6.8 และ 3.4 แต่คูณด้วย 68 และ 34 ด้วยเหตุนี้ เราจึงแยกตัวเลขหลังจุดทศนิยมได้มากเท่าที่มีหลังเครื่องหมายจุลภาคในทั้งสองตัวประกอบกัน ตัวประกอบแรกหลังจุดทศนิยมจะมีหนึ่งหลัก ส่วนตัวที่สองก็มีหนึ่งตัวด้วย โดยรวมแล้ว เราแยกตัวเลขสองหลักหลังจุดทศนิยม ดังนั้นเราจึงได้คำตอบสุดท้าย: 6.8∙3.4=23.12

การคูณทศนิยมโดยไม่ต้องคำนึงถึงเครื่องหมายจุลภาค ที่จริงแล้ว แทนที่จะคูณ 36.85 ด้วย 1.14 เรากลับคูณ 3685 ด้วย 14 เราได้ 51590 ตอนนี้ในผลลัพธ์นี้ เราจำเป็นต้องแยกตัวเลขให้มากที่สุดเท่าที่จะเป็นไปได้ด้วยลูกน้ำ เนื่องจากทั้งสองตัวประกอบกัน ตัวเลขตัวแรกมีตัวเลขสองหลักหลังจุดทศนิยม ตัวที่สองมีหนึ่งตัว โดยรวมแล้วเราคั่นตัวเลขสามหลักด้วยลูกน้ำ เนื่องจากมีศูนย์ที่ส่วนท้ายของรายการหลังจุดทศนิยม เราจึงไม่เขียนมันเป็นคำตอบ: 36.85∙1.4=51.59

ในการคูณทศนิยมเหล่านี้ เราจะคูณตัวเลขโดยไม่ต้องสนใจเครื่องหมายจุลภาค นั่นคือเราคูณจำนวนธรรมชาติ 2315 และ 7 เราได้ 16205 ในจำนวนนี้ จะต้องแยกตัวเลขสี่หลักหลังจุดทศนิยม - มากเท่ากับที่มีทั้งสองตัวประกอบกัน (สองตัวในแต่ละตัว) คำตอบสุดท้าย: 23.15∙0.07=1.6205

การคูณเศษส่วนทศนิยมด้วยจำนวนธรรมชาติก็ทำในลักษณะเดียวกัน เราคูณตัวเลขโดยไม่ต้องสนใจเครื่องหมายจุลภาคนั่นคือเราคูณ 75 ด้วย 16 ผลลัพธ์ที่ได้หลังจากเครื่องหมายจุลภาคควรมีสัญญาณมากที่สุดเท่าที่มีในทั้งสองปัจจัยรวมกัน - หนึ่งอัน ดังนั้น 75∙1.6=120.0=120

เราเริ่มการคูณเศษส่วนทศนิยมด้วยการคูณจำนวนธรรมชาติ เนื่องจากเราไม่ได้สนใจเครื่องหมายจุลภาค หลังจากนั้นเราแยกหลักหลังเครื่องหมายจุลภาคให้มากที่สุดเท่าที่มีในทั้งสองปัจจัยรวมกัน ตัวเลขแรกมีทศนิยมสองตำแหน่ง และตัวเลขที่สองมีทศนิยมสองตำแหน่ง โดยรวมแล้วควรมีตัวเลขสี่หลักหลังจุดทศนิยม: 4.72∙5.04=23.7888

ในบทเรียนที่แล้ว เราได้เรียนรู้วิธีบวกและลบเศษส่วนทศนิยม (ดูบทเรียน " การบวกและการลบเศษส่วนทศนิยม") ในเวลาเดียวกันพวกเขาประเมินว่าการคำนวณจะง่ายขึ้นมากเพียงใดเมื่อเทียบกับเศษส่วน "สองชั้น" ตามปกติ

น่าเสียดายที่ด้วยการคูณและหารเศษส่วนทศนิยม ผลกระทบนี้จะไม่เกิดขึ้น ในบางกรณี สัญลักษณ์ทศนิยมอาจทำให้การดำเนินการเหล่านี้ซับซ้อนขึ้น

ก่อนอื่น เรามาแนะนำคำจำกัดความใหม่กันก่อน เราจะพบเขาค่อนข้างบ่อย ไม่ใช่แค่ในบทเรียนนี้เท่านั้น

ส่วนสำคัญของตัวเลขคือทุกอย่างระหว่างตัวเลขตัวแรกและตัวสุดท้ายที่ไม่ใช่ศูนย์ รวมถึงตัวอย่างด้วย เรากำลังพูดถึงตัวเลขเท่านั้น จุดทศนิยมจะไม่นำมาพิจารณา

ตัวเลขที่อยู่ในส่วนสำคัญของตัวเลขเรียกว่าเลขนัยสำคัญ สามารถทำซ้ำได้และมีค่าเท่ากับศูนย์ด้วยซ้ำ

ตัวอย่างเช่น พิจารณาเศษส่วนทศนิยมหลายตัวแล้วเขียนส่วนสำคัญที่สอดคล้องกัน:

1. 91.25 → 9125 (ตัวเลขสำคัญ: 9; 1; 2; 5);
2. 0.008241 → 8241 (ตัวเลขสำคัญ: 8; 2; 4; 1);
3. 15.0075 → 150075 (ตัวเลขสำคัญ: 1; 5; 0; 0; 7; 5);
4. 0.0304 → 304 (ตัวเลขสำคัญ: 3; 0; 4);
5. 3000 → 3 (มีเลขนัยสำคัญเพียงตัวเดียว: 3)

โปรดทราบ: ศูนย์ในส่วนสำคัญของตัวเลขจะไม่ไปไหนเลย เราได้พบสิ่งที่คล้ายกันแล้วเมื่อเราเรียนรู้ที่จะแปลงเศษส่วนทศนิยมเป็นเศษส่วนสามัญ (ดูบทเรียน “ เศษส่วนทศนิยม”)

ประเด็นนี้สำคัญมากและมีข้อผิดพลาดเกิดขึ้นที่นี่บ่อยครั้งจนฉันจะเผยแพร่การทดสอบในหัวข้อนี้ในอนาคตอันใกล้นี้ อย่าลืมฝึกฝน! และเราซึ่งมีแนวคิดเป็นส่วนสำคัญจึงจะดำเนินการตามหัวข้อของบทเรียนต่อไป

การคูณทศนิยม

การดำเนินการคูณประกอบด้วยสามขั้นตอนติดต่อกัน:

1. สำหรับแต่ละเศษส่วน ให้เขียนส่วนสำคัญลงไป คุณจะได้จำนวนเต็มธรรมดาสองตัว - โดยไม่มีตัวส่วนและจุดทศนิยม
2. คูณตัวเลขเหล่านี้ด้วยวิธีที่สะดวก โดยตรงหากตัวเลขมีขนาดเล็กหรืออยู่ในคอลัมน์ เราได้ส่วนสำคัญของเศษส่วนที่ต้องการ
3. ค้นหาว่าจุดทศนิยมเลื่อนไปที่ไหนและกี่หลักในเศษส่วนเดิมเพื่อให้ได้ส่วนที่มีนัยสำคัญที่สอดคล้องกัน ดำเนินการกะย้อนกลับในส่วนสำคัญที่ได้รับในขั้นตอนก่อนหน้า

ฉันขอเตือนคุณอีกครั้งว่าจะไม่นำศูนย์ที่ด้านข้างของส่วนสำคัญมาพิจารณา การเพิกเฉยกฎนี้ทำให้เกิดข้อผิดพลาด

1. 0.28 12.5;
2. 6.3 1.08;
3. 132.5 0.0034;
4. 0.0108 1600.5;
5. 5.25 10,000.

เราทำงานกับนิพจน์แรก: 0.28 12.5

1. มาเขียนส่วนสำคัญของตัวเลขจากนิพจน์นี้กัน: 28 และ 125;
2. ผลิตภัณฑ์ของพวกเขา: 28 125 = 3500;
3. ในตัวคูณแรก จุดทศนิยมจะถูกเลื่อนไปทางขวา 2 หลัก (0.28 → 28) และในตัวที่สอง - อีก 1 หลัก โดยรวมแล้วจำเป็นต้องเลื่อนไปทางซ้ายสามหลัก: 3500 → 3.500 = 3.5

ทีนี้มาจัดการกับนิพจน์ 6.3 1.08 กันดีกว่า

1. มาเขียนส่วนสำคัญกัน: 63 และ 108;
2. สินค้า: 63 108 = 6804;
3. อีกครั้ง เลื่อนไปทางขวาสองครั้ง: ทีละ 2 และ 1 หลัก ตามลำดับ รวมแล้ว - อีก 3 หลักทางด้านขวาดังนั้นการเปลี่ยนย้อนกลับจะเป็น 3 หลักทางซ้าย: 6804 → 6.804 คราวนี้ไม่มีศูนย์ในตอนท้าย

เราได้นิพจน์ที่สามแล้ว: 132.5 0.0034

1. ส่วนสำคัญ: 1325 และ 34;
2. ผลิตภัณฑ์ของพวกเขา: 1325 34 = 45,050;
3. ในเศษส่วนแรกจุดทศนิยมไปทางขวา 1 หลักและในส่วนที่สอง - มากถึง 4 รวม: 5 ไปทางขวา เราเลื่อนไปทางซ้าย 5: 45050 → .45050 = 0.4505 ศูนย์ถูกลบออกในตอนท้าย และเพิ่มที่ด้านหน้าเพื่อไม่ให้มีจุดทศนิยม "เปล่า"

นิพจน์ต่อไปนี้: 0.0108 1600.5

1. เราเขียนส่วนสำคัญ: 108 และ 16 005;
2. เราคูณพวกมัน: 108 16 005 = 1 728 540;
3. เรานับตัวเลขหลังจุดทศนิยม: ในตัวเลขแรกมี 4 ในวินาที - 1 รวมทั้งหมด - อีกครั้ง 5 เรามี: 1,728,540 → 17.28540 = 17.2854 ในตอนท้าย ศูนย์ "พิเศษ" ก็ถูกลบออก

สุดท้าย นิพจน์สุดท้าย: 5.25 10,000

1. ส่วนสำคัญ: 525 และ 1;
2. เราคูณพวกมัน: 525 1 = 525;
3. เศษส่วนแรกเลื่อนไปทางขวา 2 หลัก และเศษส่วนที่สองเลื่อนไปทางซ้าย 4 หลัก (10,000 → 1.0000 = 1) รวม 4 − 2 = 2 หลักทางซ้าย เราทำการย้อนกลับ 2 หลักทางด้านขวา: 525, → 52 500 (เราต้องเพิ่มศูนย์)

โปรดใส่ใจกับตัวอย่างสุดท้าย: เนื่องจากจุดทศนิยมเคลื่อนที่ไปในทิศทางที่ต่างกัน การเปลี่ยนแปลงทั้งหมดจึงเกิดจากผลต่าง นี้เป็นอย่างมาก จุดสำคัญ! นี่เป็นอีกตัวอย่างหนึ่ง:

พิจารณาตัวเลข 1.5 และ 12,500 เรามี: 1.5 → 15 (เลื่อนไปทางขวา 1) 12 500 → 125 (เลื่อน 2 ไปทางซ้าย) เรา "ก้าว" ไปทางขวา 1 หลักแล้วไปทางซ้าย 2 หลัก เป็นผลให้เราก้าวไปทางซ้าย 2 − 1 = 1 หลัก

การหารทศนิยม

การแบ่งแยกอาจเป็นปฏิบัติการที่ยากที่สุด แน่นอน ที่นี่คุณสามารถดำเนินการโดยการเปรียบเทียบกับการคูณ: หารส่วนสำคัญแล้ว "ย้าย" จุดทศนิยม แต่ในกรณีนี้ มีรายละเอียดปลีกย่อยมากมายที่ขัดขวางการประหยัดที่อาจเกิดขึ้น

ดังนั้นเรามาดูอัลกอริธึมทั่วไปที่ยาวกว่าเล็กน้อย แต่มีความน่าเชื่อถือมากกว่า:

1. แปลงทศนิยมทั้งหมดให้เป็นเศษส่วนร่วม ด้วยการฝึกฝนเพียงเล็กน้อย ขั้นตอนนี้จะใช้เวลาไม่กี่วินาที
2. หารเศษส่วนที่ได้ วิถีคลาสสิก. กล่าวอีกนัยหนึ่งให้คูณเศษส่วนแรกด้วยวินาทีที่ "กลับด้าน" (ดูบทเรียน " การคูณและการหารเศษส่วนตัวเลข");
3. หากเป็นไปได้ ให้ส่งคืนผลลัพธ์เป็นทศนิยม ขั้นตอนนี้ยังเร็วอีกด้วย เพราะบ่อยครั้งที่ตัวส่วนมีพลังเป็นสิบอยู่แล้ว

งาน. ค้นหาค่าของนิพจน์:

1. 3,51: 3,9;
2. 1,47: 2,1;
3. 6,4: 25,6:
4. 0,0425: 2,5;
5. 0,25: 0,002.

เราพิจารณาสำนวนแรก ขั้นแรก เรามาแปลงเศษส่วนโอบีเป็นทศนิยมกันก่อน:

เราทำเช่นเดียวกันกับนิพจน์ที่สอง ตัวเศษของเศษส่วนแรกจะถูกแบ่งออกเป็นตัวประกอบอีกครั้ง:

มีจุดสำคัญในตัวอย่างที่สามและสี่: หลังจากกำจัดเครื่องหมายทศนิยมแล้ว เศษส่วนที่ยกเลิกได้จะปรากฏขึ้น อย่างไรก็ตาม เราจะไม่ดำเนินการลดหย่อนนี้

ตัวอย่างสุดท้ายน่าสนใจเพราะตัวเศษของเศษส่วนที่สองเป็นจำนวนเฉพาะ ไม่มีอะไรที่จะต้องแยกตัวประกอบที่นี่ ดังนั้นเราจึงพิจารณาว่า "ว่างเปล่า":

บางครั้งการหารจะให้ผลลัพธ์เป็นจำนวนเต็ม (ฉันกำลังพูดถึงตัวอย่างสุดท้าย) ในกรณีนี้ ขั้นตอนที่สามจะไม่ดำเนินการเลย

นอกจากนี้ เมื่อทำการหาร เศษส่วนที่ “น่าเกลียด” มักจะปรากฏขึ้นซึ่งไม่สามารถแปลงเป็นทศนิยมได้ นี่คือจุดที่การหารแตกต่างจากการคูณ โดยที่ผลลัพธ์จะแสดงในรูปแบบทศนิยมเสมอ แน่นอนว่าในกรณีนี้ ขั้นตอนสุดท้ายจะไม่ดำเนินการอีกครั้ง

ให้ความสนใจกับตัวอย่างที่ 3 และ 4 ด้วย ในนั้นเราจงใจไม่ลดเศษส่วนสามัญที่ได้จากทศนิยม มิฉะนั้นจะทำให้ปัญหาผกผันซับซ้อนขึ้น โดยแสดงคำตอบสุดท้ายอีกครั้งในรูปแบบทศนิยม

ข้อควรจำ: คุณสมบัติพื้นฐานของเศษส่วน (เช่นเดียวกับกฎอื่นๆ ในคณิตศาสตร์) ในตัวมันเองไม่ได้หมายความว่าจะต้องนำไปใช้ทุกที่และทุกเวลา ในทุกโอกาส

ในบทช่วยสอนนี้ เราจะดูการดำเนินการแต่ละรายการทีละรายการ

เนื้อหาบทเรียน

การบวกทศนิยม

ดังที่เราทราบ ทศนิยมมีส่วนเป็นจำนวนเต็มและเศษส่วน เมื่อบวกทศนิยม จำนวนเต็มและเศษส่วนจะถูกบวกแยกกัน

ตัวอย่างเช่น ลองบวกทศนิยม 3.2 และ 5.3 การบวกเศษส่วนทศนิยมในคอลัมน์จะสะดวกกว่า

ขั้นแรก เราเขียนเศษส่วนทั้งสองนี้ลงในคอลัมน์ โดยส่วนที่เป็นจำนวนเต็มต้องอยู่ใต้ส่วนจำนวนเต็ม และส่วนที่เป็นเศษส่วนอยู่ใต้ส่วนที่เป็นเศษส่วน ในโรงเรียนเรียกว่าข้อกำหนดนี้ "ลูกน้ำใต้ลูกน้ำ".

ลองเขียนเศษส่วนลงในคอลัมน์โดยให้ลูกน้ำอยู่ใต้ลูกน้ำ:

เราเริ่มเพิ่มเศษส่วน: 2 + 3 \u003d 5 เราเขียนห้าส่วนในส่วนที่เป็นเศษส่วนของคำตอบ:

ตอนนี้เราบวกส่วนของจำนวนเต็ม: 3 + 5 = 8 เราเขียนแปดในส่วนจำนวนเต็มของคำตอบของเรา:

ตอนนี้เราแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้เราปฏิบัติตามกฎอีกครั้ง "ลูกน้ำใต้ลูกน้ำ":

ได้คำตอบแล้ว 8.5 ดังนั้นนิพจน์ 3.2 + 5.3 จึงเท่ากับ 8.5

ที่จริงแล้วไม่ใช่ทุกอย่างจะง่ายอย่างที่คิดเมื่อเห็นแวบแรก ที่นี่ก็มีข้อผิดพลาดเช่นกัน ซึ่งเราจะพูดถึงในตอนนี้

ตำแหน่งเป็นทศนิยม

ทศนิยมก็เหมือนกับตัวเลขทั่วไปที่มีตัวเลขเป็นของตัวเอง เหล่านี้เป็นสถานที่ที่สิบ, ที่ร้อย, ที่พัน. ในกรณีนี้ ตัวเลขจะเริ่มต้นหลังจุดทศนิยม

หลักแรกหลังจุดทศนิยมมีหน้าที่รับผิดชอบในตำแหน่งที่สิบ หลักที่สองหลังจุดทศนิยมสำหรับหลักร้อย หลักที่สามหลังจุดทศนิยมคือหลักพัน

ตัวเลขทศนิยมจะเก็บข้อมูลที่เป็นประโยชน์บางอย่าง โดยเฉพาะอย่างยิ่งพวกเขารายงานว่ามีกี่ในสิบ ร้อย และหนึ่งในพันเป็นทศนิยม

เช่น พิจารณาทศนิยม 0.345

ตำแหน่งที่ตรีตั้งอยู่นั้นเรียกว่า อันดับที่สิบ

ตำแหน่งที่ทั้งสี่ตั้งอยู่เรียกว่า อันดับที่ร้อย

ตำแหน่งที่ทั้งห้าตั้งอยู่เรียกว่า หนึ่งในพัน

ลองดูที่รูปนี้ เราจะเห็นว่าในหมวดสิบนั้นมีสาม นี่แสดงว่ามีสามในสิบของเศษส่วนทศนิยม 0.345

ถ้าเราบวกเศษส่วนแล้วเราจะได้เศษส่วนทศนิยมเดิม 0.345

จะเห็นได้ว่าตอนแรกเราได้คำตอบแต่แปลงเป็นเศษส่วนทศนิยมแล้วได้ 0.345

เมื่อบวกเศษส่วนทศนิยม จะต้องปฏิบัติตามหลักการและกฎเดียวกันกับเมื่อบวกเลขธรรมดา การบวกเศษส่วนทศนิยมเกิดขึ้นด้วยตัวเลข: ส่วนที่สิบจะถูกบวกเข้ากับหลักสิบ, หลักร้อยถึงหลักร้อย, หลักพันถึงหลักพัน

ดังนั้นการบวกเศษส่วนทศนิยมจึงต้องเป็นไปตามกฎ "ลูกน้ำใต้ลูกน้ำ". เครื่องหมายจุลภาคใต้เครื่องหมายจุลภาคจะให้ลำดับที่สิบจะเพิ่มจากสิบ, ในร้อยถึงร้อย, ในพันถึงในพัน

ตัวอย่างที่ 1ค้นหาค่าของนิพจน์ 1.5 + 3.4

ก่อนอื่น เราบวกเศษส่วน 5 + 4 = 9 เราเขียนส่วนเก้าไว้ในส่วนของเศษส่วนของคำตอบ:

ตอนนี้เราบวกจำนวนเต็มส่วนที่ 1 + 3 = 4 เราเขียนสี่ส่วนนั้นไว้ในส่วนจำนวนเต็มของคำตอบ:

ตอนนี้เราแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยลูกน้ำ ในการดำเนินการนี้ ให้ปฏิบัติตามกฎ "ลูกน้ำใต้เครื่องหมายจุลภาค" อีกครั้ง:

ได้คำตอบแล้ว 4.9. ดังนั้นค่าของนิพจน์ 1.5 + 3.4 คือ 4.9

ตัวอย่างที่ 2ค้นหาค่าของนิพจน์: 3.51 + 1.22

เราเขียนนิพจน์นี้ในคอลัมน์โดยสังเกตกฎ "ลูกน้ำใต้ลูกน้ำ"

ก่อนอื่น ให้บวกส่วนที่เป็นเศษส่วน นั่นคือส่วนที่ร้อย 1+2=3 เราเขียนสามในส่วนที่ร้อยของคำตอบของเรา:

ตอนนี้บวกหนึ่งในสิบของ 5+2=7 เราเขียนเจ็ดไว้ในส่วนที่สิบของคำตอบของเรา:

ตอนนี้บวกทั้งส่วน 3+1=4 เราเขียนทั้งสี่ข้อไว้ในคำตอบทั้งหมดของเรา:

เราแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาคโดยสังเกตกฎ "ลูกน้ำใต้เครื่องหมายจุลภาค":

ได้คำตอบแล้ว 4.73 ดังนั้นค่าของนิพจน์ 3.51 + 1.22 คือ 4.73

3,51 + 1,22 = 4,73

เช่นเดียวกับตัวเลขธรรมดา เมื่อบวกเศษส่วนทศนิยม . ในกรณีนี้คำตอบจะเขียนหนึ่งหลักและส่วนที่เหลือจะถูกโอนไปยังหลักถัดไป

ตัวอย่างที่ 3ค้นหาค่าของนิพจน์ 2.65 + 3.27

เราเขียนนิพจน์นี้ในคอลัมน์:

บวกหนึ่งในร้อยของ 5+7=12 หมายเลข 12 จะไม่พอดีกับส่วนที่ร้อยของคำตอบของเรา ดังนั้นในส่วนที่ร้อยเราเขียนหมายเลข 2 และโอนหน่วยไปยังบิตถัดไป:

ตอนนี้เราบวกหนึ่งในสิบของ 6+2=8 บวกหน่วยที่เราได้รับจากการดำเนินการครั้งก่อน เราได้ 9 เราเขียนเลข 9 ในส่วนที่สิบของคำตอบ:

ตอนนี้บวกทั้งส่วน 2+3=5 เราเขียนเลข 5 ไว้ในส่วนจำนวนเต็มของคำตอบ:

ได้คำตอบแล้ว 5.92 ดังนั้นค่าของนิพจน์ 2.65 + 3.27 คือ 5.92

2,65 + 3,27 = 5,92

ตัวอย่างที่ 4ค้นหาค่าของนิพจน์ 9.5 + 2.8

เขียนนิพจน์นี้ลงในคอลัมน์

เราบวกเศษส่วน 5 + 8 = 13 จำนวน 13 จะไม่พอดีกับเศษส่วนของคำตอบ ดังนั้นเราจึงเขียนเลข 3 ก่อนแล้วโอนหน่วยไปยังหลักถัดไป หรือโอนเป็นจำนวนเต็ม ส่วนหนึ่ง:

ตอนนี้เราบวกส่วนจำนวนเต็ม 9+2=11 บวกหน่วยที่เราได้รับจากการดำเนินการครั้งก่อน เราได้ 12 เราเขียนเลข 12 ไว้ในส่วนจำนวนเต็มของคำตอบ:

แยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

ได้คำตอบแล้ว 12.3. ดังนั้นค่าของนิพจน์ 9.5 + 2.8 คือ 12.3

9,5 + 2,8 = 12,3

เมื่อบวกเศษส่วนทศนิยม จำนวนหลักหลังจุดทศนิยมในเศษส่วนทั้งสองจะต้องเท่ากัน หากมีตัวเลขไม่เพียงพอ สถานที่เหล่านี้ในส่วนเศษส่วนจะเต็มไปด้วยศูนย์

ตัวอย่างที่ 5. ค้นหาค่าของนิพจน์: 12.725 + 1.7

ก่อนที่จะเขียนนิพจน์นี้ในคอลัมน์ เรามาทำให้จำนวนหลักหลังจุดทศนิยมในเศษส่วนทั้งสองมีค่าเท่ากันก่อน เศษส่วนทศนิยม 12.725 มีเลขสามหลักหลังจุดทศนิยม ในขณะที่เศษส่วน 1.7 มีเพียงเลขเดียว ดังนั้นในส่วนท้ายของ 1.7 คุณต้องบวกศูนย์สองตัว แล้วเราจะได้เศษส่วน 1,700. ตอนนี้คุณสามารถเขียนนิพจน์นี้ลงในคอลัมน์และเริ่มคำนวณได้:

บวกหนึ่งในพันของ 5+0=5 เราเขียนเลข 5 ในส่วนหนึ่งในพันของคำตอบ:

บวกหนึ่งในร้อยของ 2+0=2 เราเขียนหมายเลข 2 ในส่วนที่ร้อยของคำตอบ:

บวกหนึ่งในสิบของ 7+7=14 หมายเลข 14 จะไม่พอดีกับหนึ่งในสิบของคำตอบของเรา ดังนั้นเราจึงเขียนหมายเลข 4 ก่อนแล้วโอนหน่วยไปยังบิตถัดไป:

ตอนนี้เราบวกส่วนจำนวนเต็ม 12+1=13 บวกหน่วยที่เราได้รับจากการดำเนินการครั้งก่อน เราได้ 14 เราเขียนเลข 14 ไว้ในส่วนจำนวนเต็มของคำตอบ:

แยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

ได้คำตอบ 14,425. ดังนั้นค่าของนิพจน์ 12.725+1.700 คือ 14.425

12,725+ 1,700 = 14,425

การลบทศนิยม

เมื่อลบเศษส่วนทศนิยม คุณต้องปฏิบัติตามกฎเดียวกันกับการบวก: “ลูกน้ำใต้ลูกน้ำ” และ “จำนวนหลักเท่ากันหลังจุดทศนิยม”

ตัวอย่างที่ 1ค้นหาค่าของนิพจน์ 2.5 − 2.2

เราเขียนนิพจน์นี้ในคอลัมน์โดยสังเกตกฎ "ลูกน้ำใต้ลูกน้ำ":

เราคำนวณเศษส่วน 5−2=3 เราเขียนหมายเลข 3 ในส่วนที่สิบของคำตอบ:

คำนวณจำนวนเต็มส่วนที่ 2−2=0 เราเขียนศูนย์ในส่วนจำนวนเต็มของคำตอบของเรา:

แยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

เราได้คำตอบ 0.3 ดังนั้นค่าของนิพจน์ 2.5 − 2.2 จึงเท่ากับ 0.3

2,5 − 2,2 = 0,3

ตัวอย่างที่ 2ค้นหาค่าของนิพจน์ 7.353 - 3.1

นิพจน์นี้มีจำนวนหลักหลังจุดทศนิยมต่างกัน ในเศษส่วน 7.353 มีตัวเลขสามหลักหลังจุดทศนิยม และในเศษส่วน 3.1 มีเพียงตัวเลขเดียว ซึ่งหมายความว่าในเศษส่วน 3.1 ต้องเพิ่มศูนย์สองตัวต่อท้ายเพื่อให้จำนวนหลักในเศษส่วนทั้งสองเท่ากัน แล้วเราจะได้ 3,100.

ตอนนี้คุณสามารถเขียนนิพจน์นี้ลงในคอลัมน์แล้วคำนวณได้:

ได้คำตอบ 4,253. ดังนั้นค่าของนิพจน์ 7.353 − 3.1 คือ 4.253

7,353 — 3,1 = 4,253

เช่นเดียวกับตัวเลขทั่วไป บางครั้งคุณจะต้องยืมบิตหนึ่งจากบิตที่อยู่ติดกันหากการลบเป็นไปไม่ได้

ตัวอย่างที่ 3จงหาค่าของนิพจน์ 3.46 − 2.39

ลบหนึ่งในร้อยของ 6−9 จากเลข 6 อย่าลบเลข 9 ดังนั้นคุณต้องนำหน่วยจากหลักที่อยู่ติดกัน เมื่อยืมมาหนึ่งตัวจากหลักข้างเคียง เลข 6 จะกลายเป็นเลข 16 ตอนนี้เราสามารถคำนวณหนึ่งในร้อยของ 16−9=7 ได้แล้ว เราเขียนเจ็ดไว้ในส่วนที่ร้อยของคำตอบของเรา:

ตอนนี้ลบสิบ. เนื่องจากเราเอาหน่วยหนึ่งในสิบมาหนึ่งหน่วย ตัวเลขที่อยู่ในนั้นจึงลดลงหนึ่งหน่วย กล่าวอีกนัยหนึ่ง อันดับที่สิบตอนนี้ไม่ใช่หมายเลข 4 แต่เป็นหมายเลข 3 ลองคำนวณหนึ่งในสิบของ 3−3=0 กัน เราเขียนศูนย์ในส่วนที่สิบของคำตอบของเรา:

ตอนนี้ลบส่วนจำนวนเต็ม 3−2=1 เราเขียนหน่วยในส่วนจำนวนเต็มของคำตอบของเรา:

แยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

ได้คำตอบแล้ว 1.07. ดังนั้นค่าของนิพจน์ 3.46−2.39 จึงเท่ากับ 1.07

3,46−2,39=1,07

ตัวอย่างที่ 4. ค้นหาค่าของนิพจน์ 3−1.2

ตัวอย่างนี้ลบทศนิยมจากจำนวนเต็ม ลองเขียนนิพจน์นี้ในคอลัมน์โดยให้ส่วนจำนวนเต็มของเศษส่วนทศนิยม 1.23 อยู่ใต้เลข 3

ทีนี้ลองทำให้จำนวนหลักหลังจุดทศนิยมเท่ากัน เมื่อต้องการทำเช่นนี้ หลังจากหมายเลข 3 ให้ใส่ลูกน้ำและเพิ่มศูนย์หนึ่งตัว:

ตอนนี้ลบสิบ: 0−2 อย่าลบเลข 2 จากศูนย์ ดังนั้น คุณต้องนำหน่วยจากหลักที่อยู่ติดกัน โดยการยืมหนึ่งจากหลักที่อยู่ติดกัน 0 จะกลายเป็นเลข 10 ตอนนี้คุณสามารถคำนวณหนึ่งในสิบของ 10−2=8 ได้ เราเขียนแปดในส่วนสิบของคำตอบของเรา:

ตอนนี้ลบส่วนทั้งหมดออก เมื่อก่อนเลข 3 อยู่ในจำนวนเต็ม แต่เรายืมมาหนึ่งหน่วย เป็นผลให้มันกลายเป็นเลข 2 ดังนั้นเราจึงลบ 1 จาก 2 2−1=1 เราเขียนหน่วยในส่วนจำนวนเต็มของคำตอบของเรา:

แยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยเครื่องหมายจุลภาค:

ได้คำตอบแล้ว 1.8. ดังนั้นค่าของนิพจน์ 3−1.2 คือ 1.8

การคูณทศนิยม

การคูณทศนิยมเป็นเรื่องง่ายและสนุกด้วยซ้ำ หากต้องการคูณทศนิยม คุณต้องคูณมันเหมือนตัวเลขปกติ โดยไม่สนใจลูกน้ำ

เมื่อได้รับคำตอบแล้ว จำเป็นต้องแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้ คุณต้องนับจำนวนหลักหลังจุดทศนิยมในเศษส่วนทั้งสอง จากนั้นนับจำนวนหลักทางด้านขวาในคำตอบแล้วใส่ลูกน้ำ

ตัวอย่างที่ 1ค้นหาค่าของนิพจน์ 2.5 × 1.5

เราคูณเศษส่วนทศนิยมเหล่านี้เป็นตัวเลขธรรมดา โดยไม่สนใจเครื่องหมายจุลภาค หากต้องการเพิกเฉยต่อเครื่องหมายจุลภาค คุณสามารถจินตนาการได้ว่าเครื่องหมายเหล่านั้นหายไปเลย:

เราได้ 375 ในจำนวนนี้ จำเป็นต้องแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้คุณต้องนับจำนวนหลักหลังจุดทศนิยมเป็นเศษส่วน 2.5 และ 1.5 ในเศษส่วนแรกจะมีหนึ่งหลักหลังจุดทศนิยม ในเศษส่วนที่สองก็มีหนึ่งด้วย รวมเป็นตัวเลขสองตัว

เรากลับไปที่หมายเลข 375 และเริ่มเคลื่อนจากขวาไปซ้าย เราต้องนับสองหลักจากทางขวาและใส่ลูกน้ำ:

ได้คำตอบแล้ว 3.75 ดังนั้นค่าของนิพจน์ 2.5 × 1.5 คือ 3.75

2.5 x 1.5 = 3.75

ตัวอย่างที่ 2ค้นหาค่าของนิพจน์ 12.85 × 2.7

ลองคูณทศนิยมเหล่านี้โดยไม่สนใจลูกน้ำ:

เราได้ 34695 ในจำนวนนี้ คุณต้องแยกเศษส่วนทั้งหมดออกจากเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้คุณต้องคำนวณจำนวนหลักหลังจุดทศนิยมเป็นเศษส่วน 12.85 และ 2.7 ในเศษส่วน 12.85 มีตัวเลขสองหลักหลังจุดทศนิยม ในเศษส่วน 2.7 มีหนึ่งหลัก - รวมเป็นสามหลัก

เรากลับไปที่หมายเลข 34695 และเริ่มย้ายจากขวาไปซ้าย เราต้องนับสามหลักจากทางขวาและใส่ลูกน้ำ:

ได้คำตอบ 34,695. ดังนั้นค่าของนิพจน์ 12.85 × 2.7 คือ 34.695

12.85 × 2.7 = 34.695

การคูณทศนิยมด้วยจำนวนปกติ

บางครั้งมีสถานการณ์ที่คุณจำเป็นต้องคูณเศษส่วนทศนิยมด้วยจำนวนปกติ

หากต้องการคูณทศนิยมและจำนวนสามัญ คุณต้องคูณพวกมัน โดยไม่คำนึงถึงลูกน้ำในทศนิยม เมื่อได้รับคำตอบแล้ว จำเป็นต้องแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้คุณจะต้องนับจำนวนหลักหลังจุดทศนิยมเป็นเศษส่วนทศนิยมจากนั้นในคำตอบให้นับจำนวนหลักเท่ากันทางด้านขวาแล้วใส่ลูกน้ำ

เช่น คูณ 2.54 ด้วย 2

เราคูณเศษส่วนทศนิยม 2.54 ด้วยเลข 2 ปกติโดยไม่สนใจเครื่องหมายจุลภาค:

เราได้หมายเลข 508 ในจำนวนนี้ คุณต้องแยกส่วนจำนวนเต็มออกจากเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้ คุณต้องนับจำนวนหลักหลังจุดทศนิยมในเศษส่วน 2.54 เศษส่วน 2.54 มีตัวเลขสองหลักหลังจุดทศนิยม

เรากลับไปที่หมายเลข 508 และเริ่มเคลื่อนจากขวาไปซ้าย เราต้องนับสองหลักจากทางขวาและใส่ลูกน้ำ:

ได้คำตอบแล้ว 5.08. ดังนั้นค่าของนิพจน์ 2.54 × 2 คือ 5.08

2.54 x 2 = 5.08

การคูณทศนิยมด้วย 10, 100, 1,000

การคูณทศนิยมด้วย 10, 100 หรือ 1,000 จะทำในลักษณะเดียวกับการคูณทศนิยมด้วยตัวเลขปกติ จำเป็นต้องทำการคูณโดยไม่สนใจลูกน้ำในเศษส่วนทศนิยมแล้วในคำตอบให้แยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนโดยนับจำนวนหลักทางขวาเท่ากับจำนวนหลักที่อยู่หลังจุดทศนิยมในทศนิยม เศษส่วน

เช่น คูณ 2.88 ด้วย 10

ลองคูณเศษส่วนทศนิยม 2.88 ด้วย 10 โดยไม่สนใจเครื่องหมายจุลภาคในเศษส่วนทศนิยม:

เราได้ 2880 ในจำนวนนี้ คุณต้องแยกเศษส่วนทั้งหมดออกจากเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้ คุณต้องนับจำนวนหลักหลังจุดทศนิยมในเศษส่วน 2.88 เราจะเห็นว่าในเศษส่วน 2.88 มีตัวเลขสองหลักหลังจุดทศนิยม

เรากลับไปที่หมายเลข 2880 และเริ่มย้ายจากขวาไปซ้าย เราต้องนับสองหลักจากทางขวาและใส่ลูกน้ำ:

ได้คำตอบแล้ว 28.80 น. เราทิ้งศูนย์สุดท้าย - เราได้ 28.8 ดังนั้นค่าของนิพจน์ 2.88 × 10 คือ 28.8

2.88 x 10 = 28.8

มีวิธีที่สองในการคูณเศษส่วนทศนิยมด้วย 10, 100, 1,000 วิธีนี้ง่ายกว่าและสะดวกกว่ามาก ประกอบด้วยความจริงที่ว่าลูกน้ำในเศษส่วนทศนิยมเลื่อนไปทางขวาเป็นจำนวนหลักเท่าที่มีศูนย์อยู่ในตัวคูณ

ตัวอย่างเช่น ลองแก้ตัวอย่างก่อนหน้า 2.88×10 ด้วยวิธีนี้ เราจะดูตัวประกอบ 10 ทันทีโดยไม่ต้องคำนวณใดๆ เราสนใจว่ามีศูนย์กี่ตัวในนั้น เราเห็นว่ามันมีศูนย์หนึ่งตัว ตอนนี้ในเศษส่วน 2.88 เราเลื่อนจุดทศนิยมไปทางขวาหนึ่งหลัก เราได้ 28.8

2.88 x 10 = 28.8

ลองคูณ 2.88 ด้วย 100 ดูตัวประกอบ 100 ทันที เราสนใจว่ามีศูนย์กี่ตัวในนั้น เราเห็นว่ามันมีศูนย์สองตัว ตอนนี้ในเศษส่วน 2.88 เราเลื่อนจุดทศนิยมไปทางขวา 2 หลัก จะได้ 288

2.88 x 100 = 288

ลองคูณ 2.88 ด้วย 1,000 ดูตัวประกอบ 1,000 ทันที เราสนใจว่ามีศูนย์กี่ตัวในนั้น เราเห็นว่ามันมีศูนย์สามตัว ตอนนี้ในเศษส่วน 2.88 เราเลื่อนจุดทศนิยมไปทางขวาสามหลัก ไม่มีหลักที่สาม ดังนั้นเราจึงบวกศูนย์อีกตัวหนึ่ง เป็นผลให้เราได้ 2880

2.88 x 1,000 = 2880

การคูณทศนิยมด้วย 0.1 0.01 และ 0.001

การคูณทศนิยมด้วย 0.1, 0.01 และ 0.001 มีการทำงานในลักษณะเดียวกับการคูณทศนิยมด้วยทศนิยม จำเป็นต้องคูณเศษส่วนเหมือนตัวเลขธรรมดาแล้วใส่ลูกน้ำในคำตอบโดยนับหลักทางด้านขวาเท่ากับจำนวนหลักที่อยู่หลังจุดทศนิยมในเศษส่วนทั้งสอง

เช่น คูณ 3.25 ด้วย 0.1

เราคูณเศษส่วนเหล่านี้เหมือนตัวเลขธรรมดา โดยไม่สนใจเครื่องหมายจุลภาค:

เราได้ 325 ในจำนวนนี้ คุณต้องแยกเศษส่วนทั้งหมดออกจากเศษส่วนด้วยลูกน้ำ ในการทำเช่นนี้คุณต้องคำนวณจำนวนหลักหลังจุดทศนิยมเป็นเศษส่วน 3.25 และ 0.1 ในเศษส่วน 3.25 มีตัวเลขสองหลักหลังจุดทศนิยม ในเศษส่วน 0.1 มีหนึ่งหลัก รวมเป็นตัวเลขสามตัว

เรากลับไปที่หมายเลข 325 และเริ่มเคลื่อนจากขวาไปซ้าย เราต้องนับสามหลักทางด้านขวาและใส่ลูกน้ำ หลังจากนับเลขสามหลักแล้วพบว่าเลขหมด ในกรณีนี้ คุณต้องเพิ่มศูนย์หนึ่งตัวและใส่ลูกน้ำ:

เราได้คำตอบ 0.325. ดังนั้นค่าของนิพจน์ 3.25 × 0.1 คือ 0.325

3.25 x 0.1 = 0.325

มีวิธีที่สองในการคูณทศนิยมด้วย 0.1, 0.01 และ 0.001 วิธีนี้ง่ายกว่าและสะดวกกว่ามาก ประกอบด้วยข้อเท็จจริงที่ว่าลูกน้ำในเศษส่วนทศนิยมเลื่อนไปทางซ้ายตามหลักจำนวนเท่าที่มีเลขศูนย์อยู่ในตัวคูณ

ตัวอย่างเช่น ลองแก้ตัวอย่างก่อนหน้า 3.25 × 0.1 ด้วยวิธีนี้ โดยไม่ต้องคำนวณใดๆ เราจะดูปัจจัย 0.1 ทันที เราสนใจว่ามีศูนย์อยู่ในนั้นกี่ตัว. เราเห็นว่ามันมีศูนย์หนึ่งตัว ตอนนี้ในเศษส่วน 3.25 เราย้ายจุดทศนิยมไปทางซ้ายหนึ่งหลัก เลื่อนลูกน้ำไปทางซ้ายหนึ่งหลักเราจะเห็นว่าไม่มีหลักอยู่ก่อนสามหลัก ในกรณีนี้ ให้เพิ่มศูนย์หนึ่งตัวและใส่ลูกน้ำ ผลลัพธ์ที่ได้คือ 0.325

3.25 x 0.1 = 0.325

ลองคูณ 3.25 ด้วย 0.01 กัน ดูตัวคูณ 0.01 ทันที เราสนใจว่ามีศูนย์อยู่ในนั้นกี่ตัว. เราเห็นว่ามันมีศูนย์สองตัว ตอนนี้ในเศษส่วน 3.25 เราเลื่อนลูกน้ำไปทางซ้ายสองหลัก จะได้ 0.0325

3.25 x 0.01 = 0.0325

ลองคูณ 3.25 ด้วย 0.001 กัน ดูตัวคูณ 0.001 ทันที เราสนใจว่ามีศูนย์อยู่ในนั้นกี่ตัว. เราเห็นว่ามันมีศูนย์สามตัว ตอนนี้ในเศษส่วน 3.25 เราย้ายจุดทศนิยมไปทางซ้ายสามหลัก เราได้ 0.00325

3.25 × 0.001 = 0.00325

อย่าสับสนกับการคูณทศนิยมด้วย 0.1, 0.001 และ 0.001 กับการคูณ 10, 100, 1,000 ข้อผิดพลาดทั่วไปคนส่วนใหญ่

เมื่อคูณด้วย 10, 100, 1,000 ลูกน้ำจะเลื่อนไปทางขวาตามหลักจำนวนเท่าที่มีศูนย์อยู่ในตัวคูณ

และเมื่อคูณด้วย 0.1, 0.01 และ 0.001 ลูกน้ำจะเลื่อนไปทางซ้ายตามหลักจำนวนเท่าที่มีศูนย์อยู่ในตัวคูณ

หากจำยากในตอนแรก คุณสามารถใช้วิธีแรกซึ่งจะทำการคูณเช่นเดียวกับตัวเลขธรรมดา ในคำตอบ คุณจะต้องแยกส่วนจำนวนเต็มออกจากส่วนที่เป็นเศษส่วนโดยนับหลักทางด้านขวาให้มากที่สุดเท่าที่มีหลักหลังจุดทศนิยมในเศษส่วนทั้งสอง

การหารจำนวนที่น้อยกว่าด้วยจำนวนที่มากกว่า ระดับสูง.

ในบทเรียนก่อนหน้านี้บทหนึ่ง เราบอกว่าเมื่อหารจำนวนที่น้อยกว่าด้วยจำนวนที่มากกว่า จะได้เศษส่วนมาในตัวเศษคือเงินปันผล และในตัวส่วนคือตัวหาร

ตัวอย่างเช่น หากต้องการแบ่งแอปเปิ้ลหนึ่งลูกออกเป็นสอง คุณต้องเขียน 1 (แอปเปิ้ลหนึ่งลูก) ในตัวเศษ และเขียน 2 (เพื่อนสองคน) ในตัวส่วน ผลลัพธ์ที่ได้คือเศษส่วน ดังนั้นเพื่อนแต่ละคนจะได้รับแอปเปิ้ล กล่าวอีกนัยหนึ่งคือแอปเปิ้ลครึ่งลูก เศษส่วนคือคำตอบของปัญหา วิธีแยกแอปเปิ้ลหนึ่งผลระหว่างสองผล

ปรากฎว่าคุณสามารถแก้ปัญหานี้ต่อไปได้หากคุณหาร 1 ด้วย 2 ท้ายที่สุดแล้ว แท่งเศษส่วนในเศษส่วนใดๆ ก็หมายถึงการหาร ซึ่งหมายความว่าการหารนี้สามารถหารด้วยเศษส่วนได้เช่นกัน แต่อย่างไร? เราคุ้นเคยกับความจริงที่ว่าเงินปันผลจะมากกว่าตัวหารเสมอ ในทางกลับกัน เงินปันผลน้อยกว่าตัวหาร.

ทุกอย่างจะชัดเจนถ้าเราจำไว้ว่าเศษส่วนหมายถึงการแตก หาร หาร ซึ่งหมายความว่าหน่วยสามารถแบ่งออกเป็นส่วนต่างๆ ได้มากเท่าที่คุณต้องการ ไม่ใช่แค่เพียงสองส่วนเท่านั้น

เมื่อหารจำนวนที่น้อยกว่าด้วยจำนวนที่มากกว่า จะได้เศษส่วนทศนิยม ซึ่งส่วนจำนวนเต็มจะเป็น 0 (ศูนย์) เศษส่วนสามารถเป็นอะไรก็ได้

ลองหาร 1 ด้วย 2 กัน ลองแก้ตัวอย่างนี้ด้วยมุม:

หนึ่งไม่สามารถแบ่งออกเป็นสองเช่นนั้น หากคุณถามคำถาม "หนึ่งมีกี่สอง" แล้วคำตอบจะเป็น 0 ดังนั้นในส่วนตัวเราจึงเขียน 0 และใส่ลูกน้ำ:

ตามปกติแล้ว เราจะคูณผลหารด้วยตัวหารเพื่อดึงเศษที่เหลือออกมา:

ถึงเวลาแล้วที่หน่วยสามารถแบ่งออกเป็นสองส่วนได้ หากต้องการทำสิ่งนี้ ให้เพิ่มศูนย์อีกอันทางด้านขวาของศูนย์ที่ได้รับ:

เราได้ 10. เราหาร 10 ด้วย 2 เราได้ 5. เราเขียนห้าลงในเศษส่วนของคำตอบ:

ตอนนี้เรานำส่วนที่เหลือสุดท้ายออกมาเพื่อคำนวณให้เสร็จสิ้น คูณ 5 ด้วย 2 เราได้ 10

เราได้คำตอบ 0.5 ดังนั้นเศษส่วนคือ 0.5

แอปเปิลครึ่งลูกสามารถเขียนได้โดยใช้เศษส่วนทศนิยม 0.5 หากเราเพิ่มทั้งสองซีกนี้ (0.5 และ 0.5) เราจะได้แอปเปิ้ลดั้งเดิมทั้งหมดอีกครั้ง:

ประเด็นนี้สามารถเข้าใจได้หากเราจินตนาการว่า 1 ซม. แบ่งออกเป็นสองส่วนอย่างไร ถ้าแบ่ง 1 เซนติเมตรออกเป็น 2 ส่วน จะได้ 0.5 ซม

ตัวอย่างที่ 2ค้นหาค่าของนิพจน์ 4:5

มีกี่ห้าในสี่? ไม่เลย. เราเขียนด้วยส่วนตัว 0 และใส่ลูกน้ำ:

เราคูณ 0 ด้วย 5 เราได้ 0 เราเขียน 0 ใต้เลขสี่. ลบศูนย์นี้ออกจากเงินปันผลทันที:

ตอนนี้เรามาเริ่มแบ่ง (แบ่ง) สี่ส่วนออกเป็น 5 ส่วนกัน ในการทำเช่นนี้ ทางด้านขวาของ 4 เราบวกศูนย์แล้วหาร 40 ด้วย 5 เราได้ 8 เราเขียนแปดแบบส่วนตัว

เราทำตัวอย่างให้สมบูรณ์โดยการคูณ 8 ด้วย 5 และรับ 40:

เราได้คำตอบ 0.8. ดังนั้นค่าของนิพจน์ 4: 5 คือ 0.8

ตัวอย่างที่ 3ค้นหาค่าของนิพจน์ 5: 125

ห้ามีเลข 125 กี่ตัว? ไม่เลย. เราเขียน 0 เป็นการส่วนตัวและใส่ลูกน้ำ:

เราคูณ 0 ด้วย 5 เราได้ 0 เราเขียน 0 ใต้ห้า. ลบออกจากห้า 0 ทันที

ตอนนี้เรามาเริ่มแบ่ง (แบ่ง) ห้าส่วนออกเป็น 125 ส่วนกัน เมื่อต้องการทำเช่นนี้ ทางด้านขวาของห้านี้ เราเขียนศูนย์:

หาร 50 ด้วย 125 จำนวน 125 มีกี่จำนวนใน 50? ไม่เลย. ในตัวหารเราเขียน 0 อีกครั้ง

เราคูณ 0 ด้วย 125 เราได้ 0 เราเขียนศูนย์นี้ไว้ต่ำกว่า 50 ลบ 0 ออกจาก 50 ทันที

ตอนนี้เราแบ่งตัวเลข 50 ออกเป็น 125 ส่วน เมื่อต้องการทำเช่นนี้ ทางด้านขวาของ 50 ให้เขียนศูนย์อีกอัน:

หาร 500 ด้วย 125 จำนวน 500 มี 125 จำนวนเท่าใด ในจำนวน 500 มีตัวเลข 125 สี่ตัว เราเขียนสี่ตัวเป็นการส่วนตัว:

เราทำตัวอย่างให้สมบูรณ์โดยการคูณ 4 ด้วย 125 และได้ 500

เราได้คำตอบ 0.04. ดังนั้นค่าของนิพจน์ 5: 125 คือ 0.04

การหารจำนวนโดยไม่มีเศษ

ดังนั้น ให้ใส่ลูกน้ำในผลหารหลังหน่วย เพื่อแสดงว่าการหารส่วนจำนวนเต็มสิ้นสุดแล้ว และเราไปยังส่วนที่เป็นเศษส่วน:

บวกศูนย์เข้ากับเศษ 4

ตอนนี้เราหาร 40 ด้วย 5 เราได้ 8 เราเขียนแปดแบบส่วนตัว:

40−40=0 ได้รับ 0 ในส่วนที่เหลือ การแบ่งส่วนจึงเสร็จสมบูรณ์ การหาร 9 ด้วย 5 ทำให้ได้ทศนิยม 1.8:

9: 5 = 1,8

ตัวอย่างที่ 2. หาร 84 ด้วย 5 โดยไม่มีเศษ

ขั้นแรกเราหาร 84 ด้วย 5 ตามปกติด้วยเศษ:

ได้รับในส่วนตัว 16 และอีก 4 ในยอด ตอนนี้เราหารเศษนี้ด้วย 5 เราใส่ลูกน้ำในไพรเวท และเพิ่ม 0 เข้ากับส่วนที่เหลือ 4

ตอนนี้เราหาร 40 ด้วย 5 เราได้ 8 เราเขียนเลขแปดลงในผลหารหลังจุดทศนิยม:

และทำตัวอย่างให้สมบูรณ์โดยตรวจสอบว่ายังมีเศษเหลืออยู่หรือไม่:

การหารทศนิยมด้วยจำนวนปกติ

อย่างที่เราทราบเศษส่วนทศนิยมประกอบด้วยจำนวนเต็มและเศษส่วน ในการหารเศษส่วนทศนิยมด้วยจำนวนปกติ สิ่งแรกที่คุณต้องมีคือ:

• หารส่วนจำนวนเต็มของเศษส่วนทศนิยมด้วยจำนวนนี้
• หลังจากแบ่งส่วนจำนวนเต็มแล้วคุณจะต้องใส่ลูกน้ำในส่วนส่วนตัวทันทีและทำการคำนวณต่อไปเช่นเดียวกับในการหารปกติ

ตัวอย่างเช่น ลองหาร 4.8 ด้วย 2

ลองเขียนตัวอย่างนี้เป็นมุม:

ทีนี้ลองหารทั้งหมดด้วย 2. สี่หารด้วย 2 ได้ 2. เราเขียน deuce แบบส่วนตัวและใส่ลูกน้ำทันที:

ตอนนี้เราคูณผลหารด้วยตัวหารแล้วดูว่ายังมีเศษเหลือจากการหารหรือไม่:

4−4=0 ที่เหลือ ศูนย์. เรายังไม่ได้เขียนเป็นศูนย์ เนื่องจากการแก้ปัญหายังไม่เสร็จสิ้น จากนั้นเราก็คำนวณต่อไปเช่นเดียวกับการหารปกติ เอา 8 ลงมาแล้วหารด้วย 2

8: 2 = 4 เราเขียนสี่ลงในผลหารแล้วคูณด้วยตัวหารทันที:

ได้คำตอบแล้ว 2.4. ค่านิพจน์ 4.8: 2 เท่ากับ 2.4

ตัวอย่างที่ 2ค้นหาค่าของนิพจน์ 8.43:3

เราหาร 8 ด้วย 3 เราได้ 2. ใส่ลูกน้ำหลังทั้งสองทันที:

ตอนนี้เราคูณผลหารด้วยตัวหาร 2 × 3 = 6 เราเขียนหกไว้ใต้แปดแล้วหาเศษ:

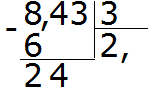
เราหาร 24 ด้วย 3 เราได้ 8. เราเขียนแปดเป็นการส่วนตัว. เราคูณมันด้วยตัวหารทันทีเพื่อหาส่วนที่เหลือของการหาร:

24−24=0 ส่วนที่เหลือเป็นศูนย์ ศูนย์ยังไม่ได้บันทึก นำเงินปันผลสามตัวสุดท้ายมาหารด้วย 3 เราจะได้ 1 คูณ 1 ด้วย 3 ทันทีเพื่อให้ตัวอย่างนี้สมบูรณ์:

ได้คำตอบ 2.81 ดังนั้นค่าของนิพจน์ 8.43: 3 จึงเท่ากับ 2.81

การหารทศนิยมด้วยทศนิยม

หากต้องการแบ่งเศษส่วนทศนิยมให้เป็นเศษส่วนทศนิยม ในตัวหารและตัวหาร ให้เลื่อนลูกน้ำไปทางขวาด้วยจำนวนหลักเดียวกันกับที่อยู่หลังจุดทศนิยมในตัวหาร แล้วหารด้วยตัวเลขปกติ

เช่น หาร 5.95 ด้วย 1.7

ลองเขียนพจน์นี้เป็นมุม

ทีนี้ ในเงินปันผลและตัวหาร เราย้ายลูกน้ำไปทางขวาด้วยจำนวนหลักเดียวกันกับที่อยู่หลังจุดทศนิยมในตัวหาร ตัวหารมีตัวเลขหนึ่งหลักหลังจุดทศนิยม ดังนั้นเราจึงต้องย้ายลูกน้ำไปทางขวาหนึ่งหลักในตัวเงินปันผลและตัวหาร. การโอน:

หลังจากเลื่อนจุดทศนิยมไปทางขวาหนึ่งหลัก เศษทศนิยม 5.95 ก็กลายเป็นเศษส่วน 59.5 และเศษส่วนทศนิยม 1.7 หลังจากเลื่อนจุดทศนิยมไปทางขวาหนึ่งหลักก็กลายเป็นเลขปกติ 17 และเรารู้วิธีหารเศษส่วนทศนิยมด้วยจำนวนปกติแล้ว การคำนวณเพิ่มเติมไม่ใช่เรื่องยาก:

ลูกน้ำถูกย้ายไปทางขวาเพื่อความสะดวกในการแบ่ง สิ่งนี้ได้รับอนุญาตเนื่องจากการคูณหรือหารเงินปันผลและตัวหารด้วยจำนวนเดียวกันผลหารจะไม่เปลี่ยนแปลง มันหมายความว่าอะไร?

นี่คือหนึ่งใน คุณสมบัติที่น่าสนใจแผนก. เรียกว่าเป็นทรัพย์สินส่วนตัว พิจารณานิพจน์ 9: 3 = 3 หากในนิพจน์นี้เงินปันผลและตัวหารถูกคูณหรือหารด้วยจำนวนเดียวกัน ผลหาร 3 จะไม่เปลี่ยนแปลง

ลองคูณเงินปันผลและตัวหารด้วย 2 แล้วดูว่าเกิดอะไรขึ้น:

(9 × 2) : (3 × 2) = 18: 6 = 3

ดังที่เห็นได้จากตัวอย่าง ผลหารไม่มีการเปลี่ยนแปลง

สิ่งเดียวกันนี้เกิดขึ้นเมื่อเราใส่ลูกน้ำในเงินปันผลและตัวหาร. ในตัวอย่างก่อนหน้านี้ เราหาร 5.91 ด้วย 1.7 เราได้ย้ายเครื่องหมายจุลภาคไปทางขวาหนึ่งหลักในตัวจ่ายเงินปันผลและตัวหาร หลังจากย้ายลูกน้ำแล้ว เศษส่วน 5.91 จะถูกแปลงเป็นเศษส่วน 59.1 และเศษส่วน 1.7 จะถูกแปลงเป็นเลขปกติ 17

อันที่จริงแล้ว ในกระบวนการนี้ มีการคูณด้วย 10 หน้าตาเป็นแบบนี้:

5.91 × 10 = 59.1

ดังนั้นจำนวนหลักหลังจุดทศนิยมในตัวหารจึงขึ้นอยู่กับว่าเงินปันผลและตัวหารจะคูณด้วยอะไร กล่าวอีกนัยหนึ่งจำนวนหลักหลังจุดทศนิยมในตัวหารจะกำหนดจำนวนหลักในการจ่ายเงินปันผลและในตัวหารเครื่องหมายจุลภาคจะถูกย้ายไปทางขวา

การหารทศนิยมด้วย 10, 100, 1,000

การหารทศนิยมด้วย 10, 100 หรือ 1,000 จะทำในลักษณะเดียวกับ ตัวอย่างเช่น ลองหาร 2.1 ด้วย 10 ลองแก้ตัวอย่างนี้ด้วยมุม:

แต่ก็มีวิธีที่สองเช่นกัน มันเบากว่า สาระสำคัญของวิธีนี้คือลูกน้ำในเงินปันผลจะถูกย้ายไปทางซ้ายตามหลักจำนวนเท่าที่มีศูนย์อยู่ในตัวหาร

ลองแก้ตัวอย่างก่อนหน้านี้ด้วยวิธีนี้ 2.1: 10. เราดูที่ตัวแบ่ง เราสนใจว่ามีศูนย์อยู่ในนั้นกี่ตัว. เราเห็นว่ามีศูนย์หนึ่งตัว ดังนั้นในการหาร 2.1 ลงตัว คุณจะต้องเลื่อนลูกน้ำไปทางซ้ายหนึ่งหลัก เราเลื่อนลูกน้ำไปทางซ้ายหนึ่งหลักแล้วดูว่าไม่มีหลักเหลือแล้ว ในกรณีนี้ เราจะเพิ่มศูนย์อีกหนึ่งตัวหน้าตัวเลข ผลลัพธ์ที่ได้คือ 0.21

ลองหาร 2.1 ด้วย 100 กัน ตัวเลข 100 มีศูนย์สองตัว ดังนั้นในการหาร 2.1 ลงตัว คุณต้องเลื่อนเครื่องหมายจุลภาคไปทางซ้ายสองหลัก:

2,1: 100 = 0,021

ลองหาร 2.1 ด้วย 1,000 กัน ตัวเลข 1,000 มีศูนย์สามตัว ดังนั้นในการหาร 2.1 ลงตัว คุณต้องเลื่อนเครื่องหมายจุลภาคไปทางซ้ายสามหลัก:

2,1: 1000 = 0,0021

การหารทศนิยมด้วย 0.1, 0.01 และ 0.001

การหารทศนิยมด้วย 0.1, 0.01 และ 0.001 จะทำในลักษณะเดียวกับ ในการจ่ายเงินปันผลและตัวหาร คุณต้องเลื่อนลูกน้ำไปทางขวาตามหลักจำนวนเท่าที่อยู่หลังจุดทศนิยมในตัวหาร

ตัวอย่างเช่น ลองหาร 6.3 ด้วย 0.1 ก่อนอื่น เราย้ายเครื่องหมายจุลภาคในเงินปันผลและในตัวหารไปทางขวาด้วยจำนวนหลักเดียวกันกับที่อยู่หลังจุดทศนิยมในตัวหาร ตัวหารมีตัวเลขหนึ่งหลักหลังจุดทศนิยม ดังนั้นเราจึงย้ายเครื่องหมายจุลภาคในเงินปันผลและในตัวหารไปทางขวาหนึ่งหลัก

หลังจากย้ายจุดทศนิยมไปทางขวาหนึ่งหลัก เศษส่วนทศนิยม 6.3 จะกลายเป็นเลขปกติ 63 และเศษส่วนทศนิยม 0.1 หลังจากเลื่อนจุดทศนิยมไปทางขวาหนึ่งหลักแล้วจะกลายเป็นหนึ่ง และการหาร 63 ด้วย 1 นั้นง่ายมาก:

ดังนั้นค่าของนิพจน์ 6.3: 0.1 จึงเท่ากับ 63

แต่ก็มีวิธีที่สองเช่นกัน มันเบากว่า สาระสำคัญของวิธีนี้คือลูกน้ำในเงินปันผลจะถูกโอนไปทางขวาเป็นจำนวนหลักเท่าที่มีศูนย์อยู่ในตัวหาร

ลองแก้ตัวอย่างก่อนหน้านี้ด้วยวิธีนี้ 6.3:0.1. มาดูตัวแบ่งกันบ้าง เราสนใจว่ามีศูนย์อยู่ในนั้นกี่ตัว. เราเห็นว่ามีศูนย์หนึ่งตัว ดังนั้นในการหาร 6.3 ลงตัว คุณจะต้องเลื่อนลูกน้ำไปทางขวาหนึ่งหลัก เราเลื่อนลูกน้ำไปทางขวาหนึ่งหลักแล้วได้ 63

ลองหาร 6.3 ด้วย 0.01 กัน ตัวหาร 0.01 มีศูนย์สองตัว ดังนั้นในการหาร 6.3 ลงตัว คุณต้องเลื่อนลูกน้ำไปทางขวาเป็นสองหลัก แต่ในการจ่ายเงินปันผลจะมีเพียงหลักเดียวหลังจุดทศนิยม ในกรณีนี้จะต้องเพิ่มศูนย์อีกหนึ่งตัวที่ส่วนท้าย เป็นผลให้เราได้ 630

ลองหาร 6.3 ด้วย 0.001 กัน. ตัวหารของ 0.001 มีศูนย์สามตัว ดังนั้นในการหาร 6.3 ลงตัว คุณต้องเลื่อนเครื่องหมายจุลภาคไปทางขวาสามหลัก:

6,3: 0,001 = 6300

งานสำหรับโซลูชันอิสระ

คุณชอบบทเรียนหรือไม่?
เข้าร่วมกับเรา กลุ่มใหม่ Vkontakte และเริ่มรับการแจ้งเตือนเกี่ยวกับบทเรียนใหม่

มาดูการกระทำต่อไปกับเศษส่วนทศนิยมกันดีกว่า ตอนนี้เราจะพิจารณาอย่างครอบคลุม การคูณทศนิยม. มาหารือกันก่อน หลักการทั่วไปการคูณทศนิยม หลังจากนั้น มาดูการคูณเศษส่วนทศนิยมด้วยเศษส่วนทศนิยม แสดงให้เห็นว่าการคูณเศษส่วนทศนิยมด้วยคอลัมน์ดำเนินการอย่างไร พิจารณาวิธีแก้ปัญหาของตัวอย่าง ต่อไป เราจะวิเคราะห์การคูณเศษส่วนทศนิยมด้วยจำนวนธรรมชาติ โดยเฉพาะ 10, 100 เป็นต้น โดยสรุป เรามาพูดถึงการคูณเศษส่วนทศนิยมด้วยเศษส่วนธรรมดาและจำนวนคละกัน

สมมติว่าในบทความนี้เราจะพูดถึงการคูณเศษส่วนทศนิยมที่เป็นบวกเท่านั้น (ดูจำนวนบวกและลบ) กรณีที่เหลือจะถูกวิเคราะห์ในบทความ การคูณจำนวนตรรกยะ และ การคูณจำนวนจริง.

การนำทางหน้า

หลักการทั่วไปของการคูณทศนิยม

เรามาพูดถึงหลักการทั่วไปที่ควรปฏิบัติเมื่อทำการคูณเศษส่วนทศนิยม

เนื่องจากทศนิยมจำกัดและเศษส่วนคาบไม่สิ้นสุดเป็นรูปแบบทศนิยมของเศษส่วนสามัญ การคูณเศษส่วนทศนิยมจึงถือเป็นการคูณเศษส่วนสามัญเป็นหลัก กล่าวอีกนัยหนึ่ง การคูณทศนิยมสุดท้าย, การคูณเศษส่วนทศนิยมสุดท้ายและเศษส่วนเป็นงวด, และ การคูณทศนิยมเป็นระยะลงมาเป็นการคูณเศษส่วนสามัญหลังจากแปลงเศษส่วนทศนิยมให้เป็นสามัญ

ลองพิจารณาตัวอย่างการประยุกต์ใช้หลักการเปล่งเสียงของการคูณเศษส่วนทศนิยม

ตัวอย่าง.

ทำการคูณทศนิยม 1.5 และ 0.75

สารละลาย.

ให้เราแทนที่เศษส่วนทศนิยมคูณด้วยเศษส่วนสามัญที่สอดคล้องกัน เนื่องจาก 1.5=15/10 และ 0.75=75/100 ดังนั้น . คุณสามารถลดเศษส่วนแล้วเลือกเศษส่วนทั้งหมดจากเศษส่วนที่ไม่ถูกต้อง แต่จะสะดวกกว่าที่ได้ผลลัพธ์ เศษส่วนทั่วไป 1 125/1 000 เขียนเป็นเศษส่วนทศนิยม 1.125.

คำตอบ:

1.5 0.75=1.125.

ควรสังเกตว่าการคูณเศษส่วนทศนิยมสุดท้ายในคอลัมน์นั้นสะดวกเราจะพูดถึงวิธีการคูณเศษส่วนทศนิยมนี้

ลองพิจารณาตัวอย่างการคูณเศษส่วนทศนิยมเป็นงวด

ตัวอย่าง.

คำนวณผลคูณของทศนิยมเป็นงวด 0,(3) และ 2,(36) .

สารละลาย.

ลองแปลงเศษส่วนทศนิยมเป็นงวดเป็นเศษส่วนสามัญ:

แล้ว . คุณสามารถแปลงเศษส่วนสามัญที่ได้ให้เป็นเศษส่วนทศนิยมได้:

คำตอบ:

0,(3) 2,(36)=0,(78) .

หากมีเศษส่วนที่ไม่ใช่คาบไม่จำกัดในเศษส่วนทศนิยมคูณแล้ว เศษส่วนคูณทั้งหมด รวมทั้งเศษส่วนที่มีขอบเขตและคาบ ควรถูกปัดเศษให้เป็นตัวเลขที่แน่นอน (ดู การปัดเศษตัวเลข) จากนั้นทำการคูณเศษส่วนทศนิยมสุดท้ายที่ได้รับหลังจากการปัดเศษ

ตัวอย่าง.

คูณทศนิยม 5.382… และ 0.2

สารละลาย.

ขั้นแรก เราปัดเศษทศนิยมที่ไม่ใช่คาบเป็นอนันต์ การปัดเศษสามารถทำได้เป็นร้อย เรามี 5.382 ... µs µ5.38 เศษส่วนทศนิยมสุดท้าย 0.2 ไม่จำเป็นต้องปัดเศษเป็นทศนิยม ดังนั้น 5.382… 0.2หยาบคาย5.38 0.2 ยังคงคำนวณผลคูณของเศษส่วนทศนิยมสุดท้าย: 5.38 0.2 \u003d 538 / 100 2 / 10 \u003d 1,076/1,000 \u003d 1.076

คำตอบ:

5.382… 0.2″1.076

การคูณเศษส่วนทศนิยมด้วยคอลัมน์

การคูณทศนิยมเทอร์มินัลสามารถทำได้โดยใช้คอลัมน์ คล้ายกับการคูณคอลัมน์ของจำนวนธรรมชาติ

มากำหนดกัน กฎการคูณเศษส่วนทศนิยม. หากต้องการคูณเศษส่วนทศนิยมด้วยคอลัมน์ คุณต้องมี:

• ละเว้นเครื่องหมายจุลภาค ทำการคูณตามกฎการคูณคอลัมน์ทั้งหมด ตัวเลขธรรมชาติ;
• ในตัวเลขผลลัพธ์ให้แยกหลักทางด้านขวาด้วยจุดทศนิยมตามที่มีจุดทศนิยมทั้งสองตัวรวมกันและหากผลคูณมีตัวเลขไม่เพียงพอจะต้องบวกจำนวนศูนย์ที่ต้องการทางด้านซ้าย

ลองพิจารณาตัวอย่างการคูณเศษส่วนทศนิยมด้วยคอลัมน์

ตัวอย่าง.

คูณทศนิยม 63.37 และ 0.12

สารละลาย.

เรามาคูณเศษส่วนทศนิยมด้วยคอลัมน์กัน ขั้นแรก เราคูณตัวเลขโดยไม่สนใจเครื่องหมายจุลภาค:

ยังคงใส่เครื่องหมายจุลภาคในผลลัพธ์ที่ได้ เธอต้องแยกตัวเลข 4 หลักทางด้านขวา เนื่องจากมีทศนิยมสี่ตำแหน่งในเศษส่วน (สองในเศษส่วน 3.37 และสองในเศษส่วน 0.12) มีตัวเลขเพียงพอแล้ว คุณจึงไม่ต้องบวกเลขศูนย์ทางด้านซ้าย มาจบการบันทึกกันเถอะ:

เป็นผลให้เราได้ 3.37 0.12 = 7.6044

คำตอบ:

3.37 0.12=7.6044.

ตัวอย่าง.

คำนวณผลคูณทศนิยม 3.2601 และ 0.0254 .

สารละลาย.

หลังจากทำการคูณด้วยคอลัมน์โดยไม่ต้องคำนึงถึงลูกน้ำ เราจะได้ภาพต่อไปนี้:

ตอนนี้ในผลิตภัณฑ์คุณต้องคั่นตัวเลข 8 หลักทางด้านขวาด้วยเครื่องหมายจุลภาคเนื่องจากจำนวนตำแหน่งทศนิยมทั้งหมดของเศษส่วนที่คูณคือแปด แต่ในผลิตภัณฑ์มีเพียง 7 หลัก ดังนั้นคุณต้องกำหนดเลขศูนย์ให้มากที่สุดเท่าที่จะเป็นไปได้ทางด้านซ้ายเพื่อให้สามารถคั่นตัวเลข 8 หลักด้วยเครื่องหมายจุลภาค ในกรณีของเรา เราต้องกำหนดศูนย์สองตัว:

ซึ่งจะทำให้การคูณเศษส่วนทศนิยมตามคอลัมน์เสร็จสมบูรณ์

คำตอบ:

3.2601 0.0254=0.08280654 .

การคูณทศนิยมด้วย 0.1, 0.01 เป็นต้น

บ่อยครั้งคุณต้องคูณทศนิยมด้วย 0.1, 0.01 และอื่นๆ ดังนั้นจึงแนะนำให้กำหนดกฎสำหรับการคูณเศษส่วนทศนิยมด้วยตัวเลขเหล่านี้ซึ่งเป็นไปตามหลักการคูณเศษส่วนทศนิยมที่กล่าวถึงข้างต้น

ดังนั้น, การคูณทศนิยมที่กำหนดด้วย 0.1, 0.01, 0.001 และอื่นๆให้เศษส่วนที่ได้รับจากต้นฉบับหากในรายการเครื่องหมายจุลภาคถูกย้ายไปทางซ้ายด้วย 1, 2, 3 และตัวเลขอื่น ๆ ตามลำดับและหากมีตัวเลขไม่เพียงพอที่จะย้ายเครื่องหมายจุลภาคคุณต้อง เพื่อเพิ่ม จำนวนที่ต้องการศูนย์

ตัวอย่างเช่น หากต้องการคูณเศษส่วนทศนิยม 54.34 ด้วย 0.1 คุณต้องย้ายจุดทศนิยมไปทางซ้าย 1 หลักในเศษส่วน 54.34 และคุณจะได้เศษส่วน 5.434 นั่นคือ 54.34 0.1 \u003d 5.434 ลองมาอีกตัวอย่างหนึ่ง คูณเศษส่วนทศนิยม 9.3 ด้วย 0.0001 ในการทำเช่นนี้เราต้องย้ายเครื่องหมายจุลภาค 4 หลักไปทางซ้ายในเศษส่วนทศนิยมคูณ 9.3 แต่บันทึกของเศษส่วน 9.3 ไม่มีอักขระจำนวนดังกล่าว ดังนั้นเราจึงต้องกำหนดเลขศูนย์ให้มากที่สุดเท่าที่จะเป็นไปได้ในบันทึกของเศษส่วน 9.3 ทางด้านซ้ายเพื่อที่เราจะได้โอนเครื่องหมายจุลภาคเป็นตัวเลข 4 หลักได้อย่างง่ายดาย เรามี 9.3 0.0001 \u003d 0.00093

โปรดทราบว่ากฎที่ประกาศสำหรับการคูณเศษส่วนทศนิยมด้วย 0.1, 0.01, ... ก็ใช้ได้กับเศษส่วนทศนิยมอนันต์เช่นกัน ตัวอย่างเช่น 0,(18) 0.01=0.00(18) หรือ 93.938… 0.1=9.3938…

การคูณทศนิยมด้วยจำนวนธรรมชาติ

ที่แกนกลางของมัน การคูณทศนิยมด้วยจำนวนธรรมชาติก็ไม่ต่างจากการคูณทศนิยมด้วยทศนิยม

วิธีที่สะดวกที่สุดในการคูณเศษส่วนทศนิยมจำกัดด้วยจำนวนธรรมชาติด้วยคอลัมน์ ในขณะที่คุณควรปฏิบัติตามกฎสำหรับการคูณด้วยคอลัมน์เศษส่วนทศนิยมที่กล่าวถึงในย่อหน้าใดย่อหน้าหนึ่ง

ตัวอย่าง.

คำนวณผลคูณ 15 2.27 .

สารละลาย.

ลองคูณจำนวนธรรมชาติด้วยเศษส่วนทศนิยมในคอลัมน์:

คำตอบ:

15 2.27=34.05.

เมื่อคูณเศษส่วนทศนิยมเป็นคาบด้วยจำนวนธรรมชาติ เศษส่วนคาบควรถูกแทนที่ด้วยเศษส่วนสามัญ

ตัวอย่าง.

คูณเศษส่วนทศนิยม 0,(42) ด้วยจำนวนธรรมชาติ 22

สารละลาย.

ขั้นแรก ให้แปลงทศนิยมเป็นงวดเป็นเศษส่วนร่วม:

ทีนี้มาคูณกัน: . ผลลัพธ์ทศนิยมนี้คือ 9,(3)

คำตอบ:

0,(42) 22=9,(3) .

และเมื่อคูณเศษส่วนทศนิยมที่ไม่ใช่คาบเป็นอนันต์ด้วยจำนวนธรรมชาติ คุณต้องปัดเศษก่อน

ตัวอย่าง.

คูณ 4 2.145….

สารละลาย.

เมื่อปัดเศษทศนิยมอนันต์ดั้งเดิมให้เป็นร้อยให้เป็นร้อย เราจะได้การคูณของจำนวนธรรมชาติและเศษส่วนทศนิยมสุดท้าย เรามี 4 2.145…µ4 2.15=8.60

คำตอบ:

4 2.145…หยาบคาย8.60

การคูณทศนิยมด้วย 10, 100, ...

บ่อยครั้งที่คุณต้องคูณเศษส่วนทศนิยมด้วย 10, 100, ... ดังนั้นจึงขอแนะนำให้พิจารณากรณีเหล่านี้โดยละเอียด

มาส่งเสียงกันเถอะ กฎสำหรับการคูณทศนิยมด้วย 10, 100, 1,000 เป็นต้นเมื่อคูณเศษส่วนทศนิยมด้วย 10, 100, ... ในรายการคุณจะต้องเลื่อนลูกน้ำไปทางขวาด้วย 1, 2, 3, ... หลักตามลำดับและทิ้งศูนย์พิเศษทางด้านซ้าย หากมีตัวเลขไม่เพียงพอในบันทึกของเศษส่วนคูณเพื่อโอนลูกน้ำคุณจะต้องเพิ่มจำนวนศูนย์ที่ต้องการทางด้านขวา

ตัวอย่าง.

คูณทศนิยม 0.0783 ด้วย 100

สารละลาย.

ลองโอนเศษส่วน 0.0783 ไปทางขวาสองหลักลงในบันทึก แล้วเราจะได้ 007.83 ปล่อยศูนย์สองตัวทางซ้าย เราจะได้เศษส่วนทศนิยม 7.38 ดังนั้น 0.0783 100=7.83

คำตอบ:

0.0783 100=7.83

ตัวอย่าง.

คูณเศษส่วนทศนิยม 0.02 ด้วย 10,000

สารละลาย.

หากต้องการคูณ 0.02 ด้วย 10,000 เราต้องเลื่อนเครื่องหมายจุลภาค 4 หลักไปทางขวา แน่นอนว่าในบันทึกเศษส่วน 0.02 มีตัวเลขไม่เพียงพอที่จะโอนเครื่องหมายจุลภาคเป็น 4 หลัก ดังนั้นเราจะบวกเลขศูนย์สองสามตัวทางด้านขวาเพื่อให้สามารถโอนเครื่องหมายจุลภาคได้ ในตัวอย่างของเรา แค่เพิ่มศูนย์สามตัวก็เพียงพอแล้ว เรามี 0.02000 หลังจากย้ายเครื่องหมายจุลภาคเราจะได้รายการ 00200.0 เมื่อปล่อยเลขศูนย์ทางด้านซ้าย เราจะได้เลข 200.0 ซึ่งเท่ากับเลขธรรมชาติ 200 ซึ่งเป็นผลมาจากการคูณเศษส่วนทศนิยม 0.02 ด้วย 10,000

§ 1 การใช้กฎสำหรับการคูณเศษส่วนทศนิยม

ในบทนี้ คุณจะได้แนะนำและเรียนรู้วิธีใช้กฎการคูณเศษส่วนทศนิยมและกฎการคูณเศษส่วนทศนิยมด้วยหน่วยหลัก เช่น 0.1, 0.01 เป็นต้น นอกจากนี้เราจะพิจารณาคุณสมบัติของการคูณเมื่อค้นหาค่าของนิพจน์ที่มีเศษส่วนทศนิยม

มาแก้ปัญหากันเถอะ:

ความเร็วรถ 59.8 กม./ชม.

รถจะเดินทางได้ไกลแค่ไหนใน 1.3 ชั่วโมง?

ดังที่คุณทราบ ในการค้นหาเส้นทาง คุณต้องคูณความเร็วตามเวลา เช่น 59.8 คูณ 1.3

มาเขียนตัวเลขในคอลัมน์และเริ่มคูณโดยไม่ต้องสังเกตลูกน้ำ: 8 คูณ 3 จะเป็น 24, 4 เราเขียน 2 ในใจ, 3 คูณ 9 เป็น 27, บวก 2, เราได้ 29, เขียน 9, 2 ใน จิตใจของเรา ตอนนี้เราคูณ 3 ด้วย 5 มันจะเป็น 15 แล้วบวกอีก 2 เราได้ 17

ไปที่บรรทัดที่สอง: 1 คูณ 8 ได้ 8, 1 คูณ 9 ได้ 9, 1 คูณ 5 ได้ 5 เพิ่มสองบรรทัดนี้ เราจะได้ 4, 9+8 คือ 17, 7 เขียน 1 ไว้ในหัว, 7 +9 คือ 16 บวก 1 มันจะเป็น 17, 7 เราเขียน 1 ในใจ, 1+5 บวก 1 เราได้ 7.

ทีนี้มาดูกันว่าเศษส่วนทศนิยมทั้งสองมีทศนิยมกี่ตำแหน่ง! เศษส่วนแรกมีหนึ่งหลักหลังจุดทศนิยม และเศษส่วนที่สองมีหนึ่งหลักหลังจุดทศนิยม รวมเป็นสองหลัก ดังนั้นทางด้านขวาในผลลัพธ์คุณจะต้องนับตัวเลขสองหลักและใส่ลูกน้ำเช่น จะเป็น 77.74 เมื่อคูณ 59.8 ด้วย 1.3 เราได้ 77.74. ดังนั้นคำตอบของโจทย์คือ 77.74 กม.

ดังนั้น ในการคูณเศษส่วนทศนิยม 2 ตัว คุณต้องมี:

ขั้นแรก: ทำการคูณโดยไม่สนใจเครื่องหมายจุลภาค

ประการที่สอง: ในผลลัพธ์ที่ได้ ให้คั่นด้วยเครื่องหมายจุลภาคตามจำนวนหลักทางด้านขวาเท่ากับที่อยู่หลังเครื่องหมายจุลภาคในทั้งสองปัจจัยรวมกัน

หากผลลัพธ์มีตัวเลขน้อยกว่าที่จำเป็นในการคั่นด้วยเครื่องหมายจุลภาค จะต้องกำหนดให้มีศูนย์หนึ่งตัวหรือมากกว่านั้นอยู่ข้างหน้า

ตัวอย่างเช่น: 0.145 คูณ 0.03 เราได้ 435 ในผลคูณ และเราต้องคั่นตัวเลข 5 หลักทางด้านขวาด้วยเครื่องหมายจุลภาค ดังนั้นเราจึงเพิ่มศูนย์อีก 2 ตัวก่อนหมายเลข 4 ใส่ลูกน้ำแล้วเพิ่มศูนย์อีกหนึ่งตัว เราได้คำตอบ 0.00435

§ 2 คุณสมบัติของการคูณเศษส่วนทศนิยม

เมื่อคูณเศษส่วนทศนิยม คุณสมบัติการคูณเดียวกันกับจำนวนธรรมชาติจะยังคงอยู่ มาทำงานบางอย่างกันเถอะ

งานหมายเลข 1:

ลองแก้ตัวอย่างนี้โดยใช้คุณสมบัติการกระจายของการคูณเทียบกับการบวก

5.7 (ปัจจัยร่วม) จะถูกนำออกจากวงเล็บ ส่วน 3.4 บวก 0.6 จะยังคงอยู่ในวงเล็บ ค่าของผลรวมนี้คือ 4 และตอนนี้ 4 ต้องคูณด้วย 5.7 เราได้ 22.8

งานหมายเลข 2:

ลองใช้สมบัติการสับเปลี่ยนของการคูณกัน

ก่อนอื่นเราคูณ 2.5 ด้วย 4 เราได้จำนวนเต็ม 10 ตัว และตอนนี้เราต้องคูณ 10 ด้วย 32.9 และเราได้ 329.

นอกจากนี้ เมื่อคูณเศษส่วนทศนิยม คุณจะสังเกตเห็นสิ่งต่อไปนี้:

เมื่อคูณตัวเลขด้วยเศษส่วนทศนิยมที่ไม่เหมาะสม เช่น มากกว่าหรือเท่ากับ 1 จะเพิ่มหรือไม่เปลี่ยนแปลง เช่น

เมื่อคูณตัวเลขด้วยเศษส่วนทศนิยมที่เหมาะสม เช่น น้อยกว่า 1 ก็จะลดลง เช่น

ลองแก้ตัวอย่าง:

23.45 คูณ 0.1

เราต้องคูณ 2,345 ด้วย 1 และแยกลูกน้ำสามตัวออกจากทางขวา เราจะได้ 2.345.

ทีนี้ลองแก้อีกตัวอย่างหนึ่ง: 23.45 หารด้วย 10 เราต้องย้ายลูกน้ำไปทางซ้ายหนึ่งตำแหน่ง เพราะ 1 ศูนย์ในหน่วยบิต เราได้ 2.345

จากตัวอย่างทั้งสองนี้ เราสามารถสรุปได้ว่าการคูณทศนิยมด้วย 0.1, 0.01, 0.001 ฯลฯ หมายถึงการหารตัวเลขด้วย 10, 100, 1,000 เป็นต้น กล่าวคือ ในเศษส่วนทศนิยม ให้เลื่อนจุดทศนิยมไปทางซ้ายตามหลักหลักเท่ากับมีศูนย์อยู่หน้า 1 ในตัวคูณ

เมื่อใช้กฎที่ได้รับเราจะค้นหาค่าของผลิตภัณฑ์:

13.45 คูณ 0.01

หน้าเลข 1 มีศูนย์ 2 ตัว ดังนั้นเราจึงเลื่อนลูกน้ำไปทางซ้าย 2 หลัก จะได้ 0.1345

0.02 คูณ 0.001

ด้านหน้าหมายเลข 1 มีศูนย์ 3 ตัว ซึ่งหมายความว่าเราเลื่อนลูกน้ำไปทางซ้ายสามหลัก เราจะได้ 0.00002

ดังนั้น ในบทเรียนนี้ คุณได้เรียนรู้วิธีคูณเศษส่วนทศนิยมแล้ว ในการทำเช่นนี้ คุณเพียงแค่ต้องทำการคูณโดยไม่สนใจเครื่องหมายจุลภาค และในผลคูณที่ได้ ให้แยกตัวเลขทางขวาให้มากที่สุดเท่าที่จะเป็นไปได้ด้วยเครื่องหมายจุลภาค เช่นเดียวกับที่อยู่หลังเครื่องหมายจุลภาคในทั้งสองปัจจัยร่วมกัน นอกจากนี้ยังได้ทำความคุ้นเคยกับกฎการคูณเศษส่วนทศนิยมด้วย 0.1, 0.01 เป็นต้น และยังได้พิจารณาคุณสมบัติของการคูณเศษส่วนทศนิยมด้วย

รายการวรรณกรรมที่ใช้:

1. คณิตศาสตร์ ป.5. Vilenkin N.Ya., Zhokhov V.I. และอื่นๆ. ฉบับพิมพ์ครั้งที่ 31, สเตอร์. - อ: 2013.
2. วัสดุการสอนในวิชาคณิตศาสตร์ชั้นประถมศึกษาปีที่ 5 ผู้แต่ง - Popov M.A. - ปี 2556
3. เราคำนวณโดยไม่มีข้อผิดพลาด ทำงานแบบทดสอบตนเองในวิชาคณิตศาสตร์เกรด 5-6 ผู้แต่ง - Minaeva S.S. - ปี 2557
4. สื่อการสอนวิชาคณิตศาสตร์ ชั้นประถมศึกษาปีที่ 5 ผู้เขียน: Dorofeev G.V., Kuznetsova L.V. - 2010
5. ควบคุมและ งานอิสระในวิชาคณิตศาสตร์ชั้นประถมศึกษาปีที่ 5 ผู้แต่ง - Popov M.A. - ปี 2555
6. คณิตศาสตร์. ชั้นประถมศึกษาปีที่ 5: หนังสือเรียน สำหรับนักศึกษาสายสามัญ สถาบัน / I. I. Zubareva, A. G. Mordkovich - ฉบับที่ 9 ซีเนียร์. - อ.: นีโมซิน, 2552